

In fact there's a function in R to calculate the Five-Number summary called fivenum. In that case you get a plot of what is known as Tukey's Five-number summary: minimum, 25th percentile, median, 75th percentile and the maximum. If we set range to 0, then the whiskers will extend to the minimum and maximum values for each group. They will always capture the middle 50% of the data no matter the value of range. You'll also notice the size of the boxes didn't change. Obviously the “outlier” classification is subjective. Now we have more “outliers” for groups 1 – 3 but still none for group 4. Here we try it set to 1: boxplot(y ~ x, range=1) If you want to change how whiskers are determined, you can change the range argument in the boxplot function. The out element of the bp object contains the outliers while the group element contains the outliers' respective groups. The first element, stats, contains the plotted points in each group. We see the bp object is a list with 6 different elements. Just call the boxplot as you normally would and save to a variable. When you create a boxplot in R, you can actually create an object that contains the plotted data. Group 4 does not appear to have outliers. (I say “appear to be single” because technically we could have overplotting.) We might think of these as outliers, data points that are too big or too small compared to the rest of the data. And the points beyond the distance are plotted as single points.įor groups 1 through 3, there appear to be single points beyond the whiskers. If there are points beyond that distance, the largest point that does not exceed that distance becomes the whisker.
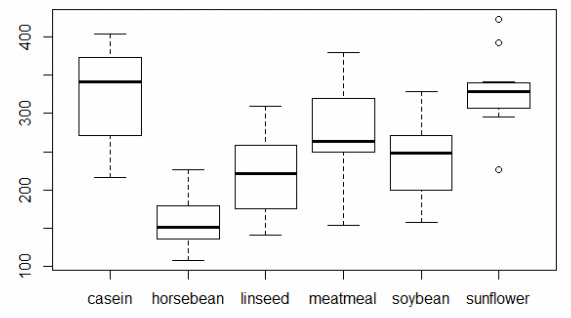
If no points exceed that distance, then the whiskers are simply the minimum and maximum values. What is that certain distance? By default in R, it's \(1.5 \times IQR\). That is, these are the minimum and maximum values that do not exceed a certain distance from the middle 50% of the data.
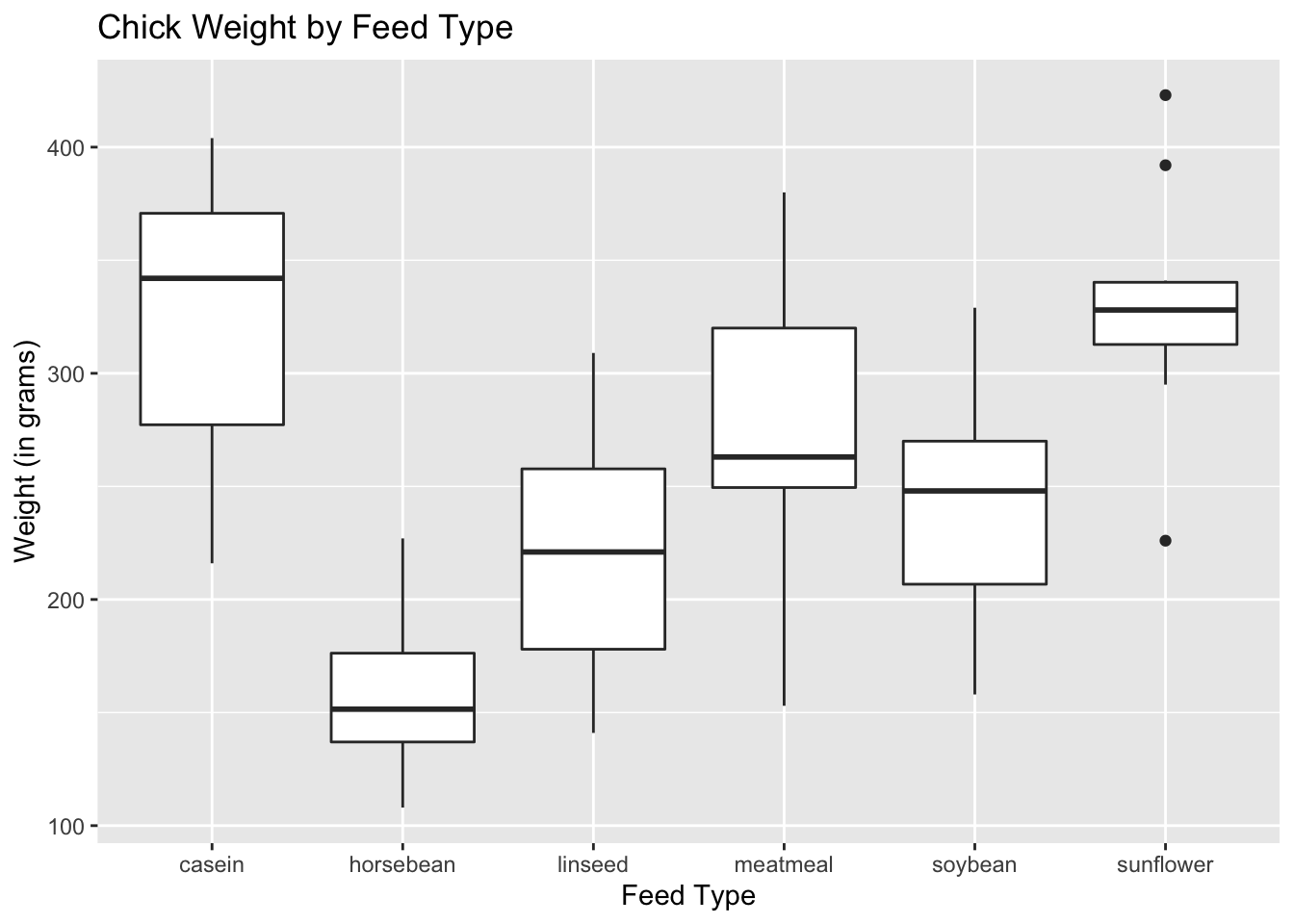
What do they represent and how are they calculated? They represent the reasonable extremes of the data. Again this makes sense given group 1 data was randomly generated from a normal distribution with a standard deviation of 5.Īnd now we come to the “whiskers”, or the flattened arrows extending out of the box. The IQR for group 1 looks to be about 5 judging from the height of the box. We see groups 1 and 2 have less variability than groups 3 and 4, which makes sense given the way we generated the data. The tops and bottoms of the boxes are referred to as “hinges”. They measure the spread of the data, sort of like standard deviation. The vertical size of the boxes are the interquartile range, or IQR. For group 1, that appears to be a shade above 20. The black lines in the “middle” of the boxes are the median values for each group. Then I generate a 4-level grouping variable. But what about the whiskers? That seems to be the part that trips people up.īefore we go further, let's make some boxplots in R: set.seed(9) The box edges are the 25th and 75th percentiles. The box itself represents the middle 50% of the data. The line in the middle of the box is the median. More often than not, however, the person I'm helping doesn't regularly use boxplots (if at all) and is not sure what to make of them.įortunately, boxplots are pretty easy to explain. They're a great way to quickly visualize the distribution of a continuous measure by some grouping variable. As a statistical consultant I frequently use boxplots.


 0 kommentar(er)
0 kommentar(er)
